数学 面積 比 984901
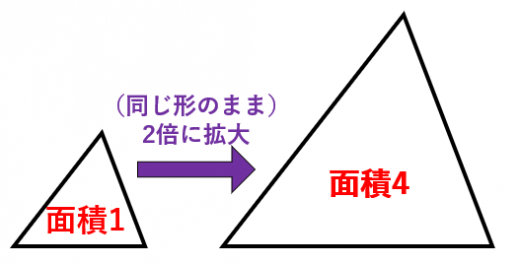
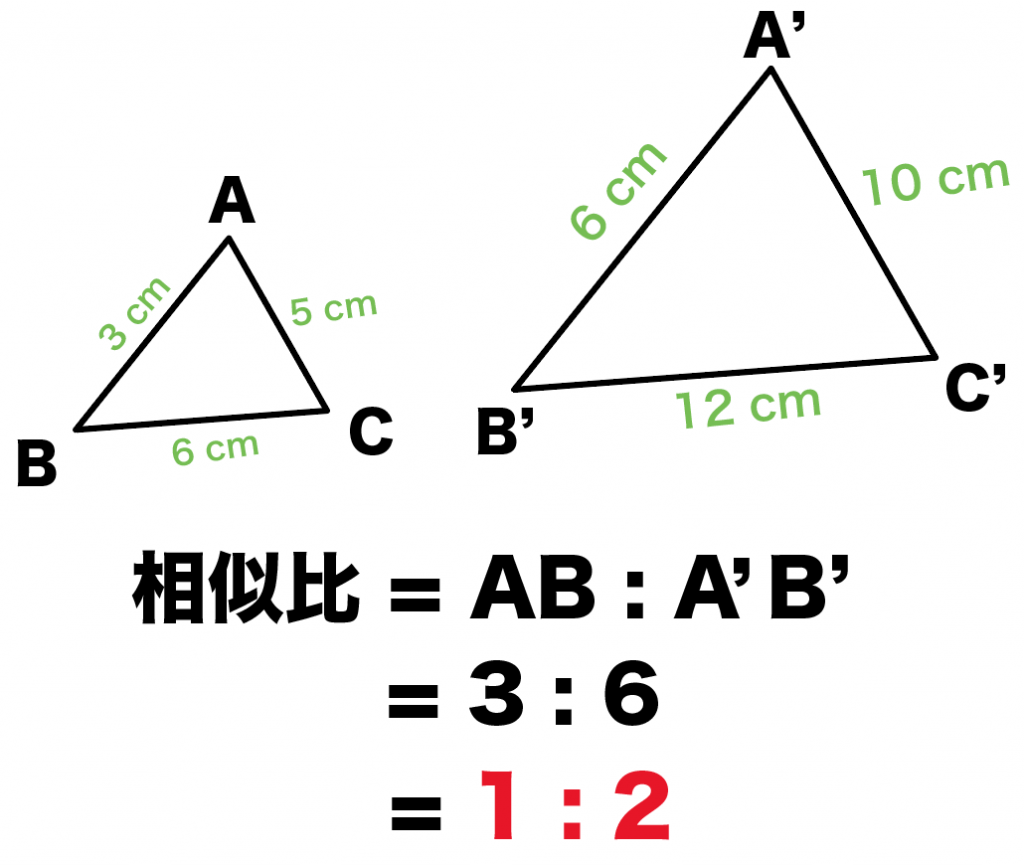
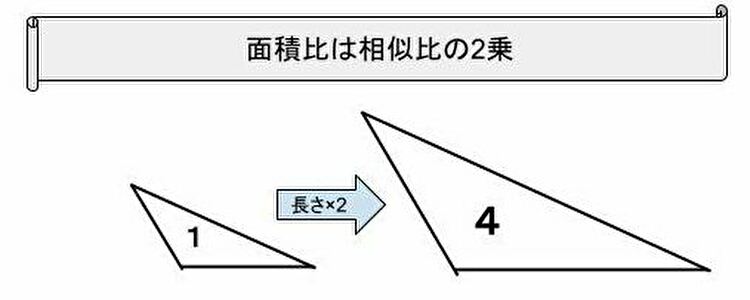
相似な図形の面積比の問題です。基本を確認して、いろいろな応用問題を解けるようにしてください。基本事項相似比が m n である図形の面積の比は,m2 n2 である。例)下のような相似な三角形がある ABCと A'B'C'の相似比は 1:2面積を求めると ABC=4 A'B'C'=16 面積比は1:4相似比が1:2のとき
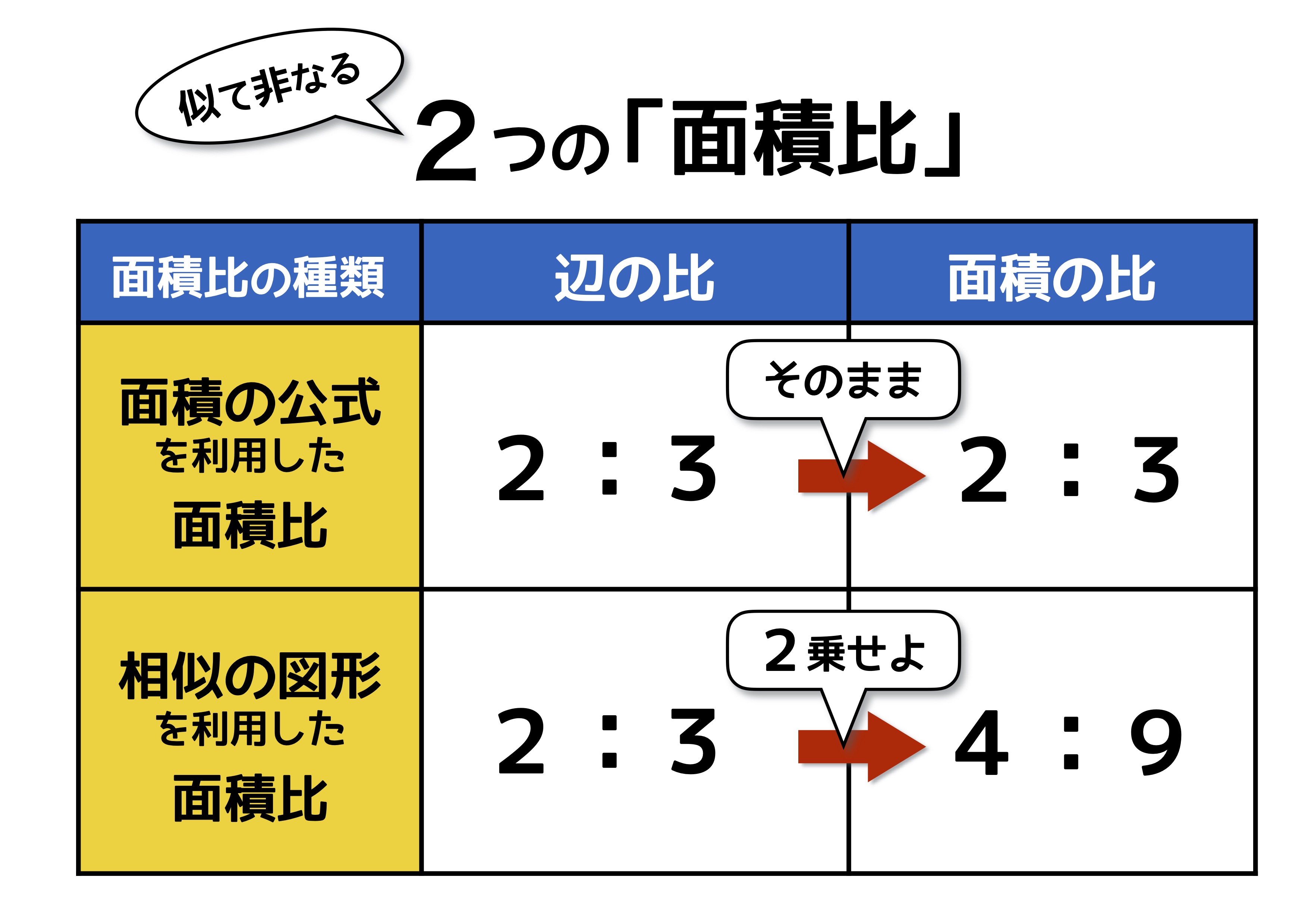
数学 面積 比-・相似比 24:36=2:3 ・面積比 22:32=4:9 ・Lサイズの値段をx 円 4:9=:x 今日は,この相似比や面積比が日常生活のどんなところで 役に立つのか考えましょう。 次の問題に取り組みましょう。 あるピザ屋では,ミックスピザの値段が, 前回の、三角形の面積比と線分比の関係パート1は、こちらにゃん 『 数学三角形の辺と面積の比について、2つの考え方をサクッとまとめました中学数学 図形 』 数学おじさん それでは今回の解説を始めるかのぉ 目次 1 数学入試で差がつく
数学 面積 比のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  | |
 |  |  |
「数学 面積 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「数学 面積 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
 | ||
「数学 面積 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「数学 面積 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「数学 面積 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「数学 面積 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「数学 面積 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「数学 面積 比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |
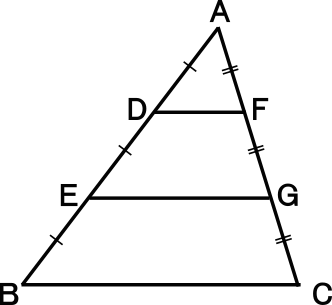
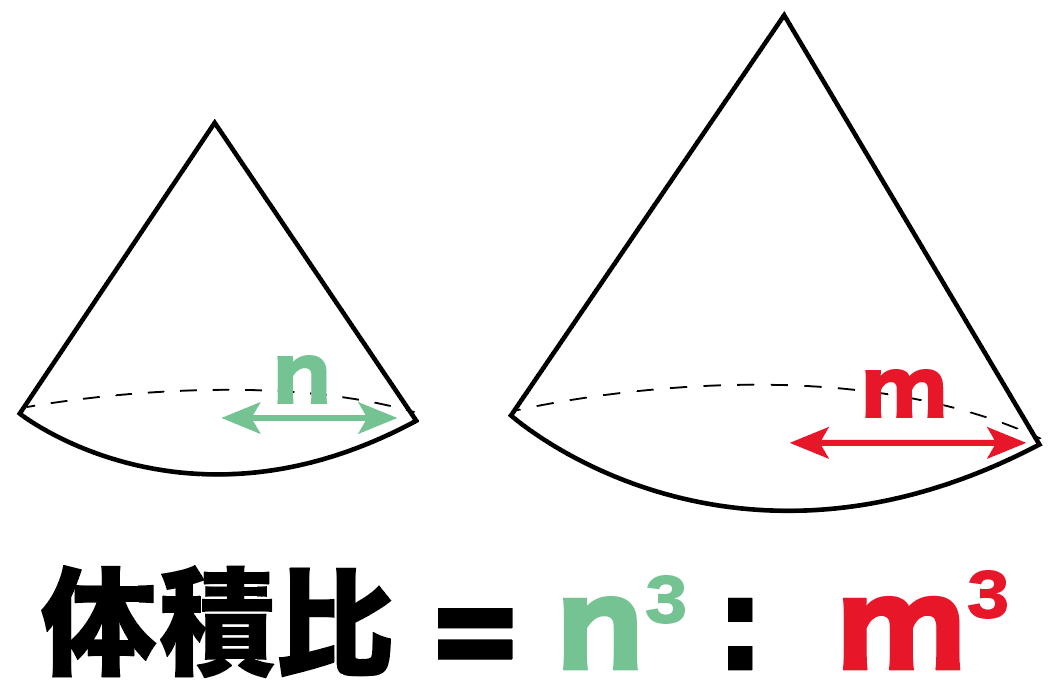
面積比は 1 2 :2 2 :3 2 = 1:4:9 ただ、それが6面あるだけですね 1×6面:4×6面:9×6面 = 1:4:9 (↑比ですので「6面」は打ち消してよい ≒ 約分) 結局「表面積比」も「面積比」同様「2乗」ですね 《 例 》 次の2つの球の表面積比は? → 相似比は、5:4 中3数学「角の二等分線定理・中点連結定理」の問題 どこよりも簡単な解き方・求め方 前回「平行線と線分の比」について学習しました この考え方と、その前に学習した「相似」を使って、図形の問題を解く際に利用する「角の二等分線定理」「中点連結定理」を一緒に見ていきま
コメント
コメントを投稿